Nested Taiji -- the art of computing and not computing

A program can only run when it fully exists. If a part of it exists not, the computation happens not. What does “exist” mean though?

This article talks about the shape of algorithms (“type”), not the implementation of them (“term”).

Nested regions in theory

We shall call a region “positive” if it “exists”; “negative” otherwise.

This idea is outside what can be described by total functions in Constructions Calculus.

A positive region is code that exists. A negative region is code to be filled in.

Nested regions in practice

An ELF file is a positive region with many negative regions with positive regions inside them. The interpreter (linker) provided by the operating system links the program together before running. The kernel fills the rest of the regions by itself.

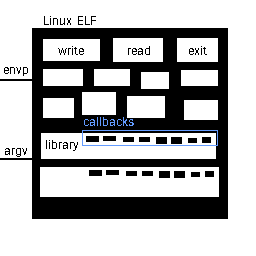
Syscalls are regions to be filled in by the kernel. Dynamic libraries used are regions that may or may not contain syscall regions or other dynamic library regions.

Nested regions in theory

Child regions of a region are not ordered. They are a unordered set.

Mathematics seem to not care which color of region exists, Yin or Yang. Yin may swap place with Yang. We only observe the boundaries of the regions are well nested – a region is either inside or it doesn’t exist, although this “exist” means differently than the negative region which “doesn’t exist” but still exists.

A curious thought: Generative algorithms may fill a region automatically. There are maybe other ways to make a negative region directly compute.

A simplified definition of a region

A region is an algorithmic fragment with a discrete number of inputs and outputs.

Each input or output term has a type, which is itself an equivalence group.

The input terms are numbered $in_i$. $i$ starts with 0.

The output terms are numbered $out_i$.

The shape of a region is the type of all inputs and all outputs of the region.

A region can be either implemented (positive) or missing (negative).

The foaming (described below) of an algorithmic syntax is othorgonal to its type system. Any type system may be used in conjunction with Taiji regions.

region shape matching

It is possible to simply introduce a region. The final algorithm may ignore whatever passed in from the created region.

To is possible to cut a region in half by spliting the outer region in half.

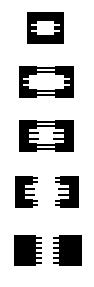
Recursive regions

Recursion is possible. If you accept the fact that algorithm blocks compose naturally like this, the combinators in To Mock a Mockingbird become typed.

For the type on the left (in the image below), it is possible to plug it with itself, or have a few of those blocks chain together into a ring.

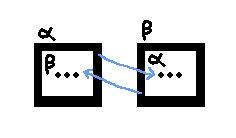
Two mutually recursive regions fit into one another.

In C, program linking is usually done by the following two steps.

1. At compile time, Part A is linked together with Part B by the ld linker.
2. At run time, Part A calls B::init(A::func) to link itself properly with Part B.

Mathematically, there is no difference between compile time linking and run time linking. Even time itself is relative.

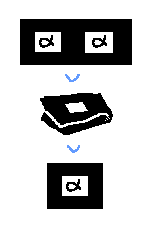
Folding regions

If you have two regions of the same shape and polarity, they can be folded into one.

Improvement over entangled algebraic effects

<details>
    <summary>You may ignore this section if you don't know algebraic effects already.</summary>
    
    In the eyes of a compiler, it is simpler to compile code written in this theory than algebraic effects.
    
    To put it simply, the idea that algebraic effects might entangle with each other is that, [a program with the ability to product effect A and effect B] has a different type from [a program with the ability to product effect A and effect B but not both at the same time]. This gets complicated fast, as more effects are added to a block of code, the combination explodes. Text-based algorithmic languages like Koka choose to not observe this fact and make every effect exclusive of CPU time. The loss of information (different ways of how effects may entangle) leads to fewer optimization opportunities by a compiler that has any sense of locality (not a "full program compiler").
</details>

Real world type checker support

Zig: No.

fn foo(foo1: @TypeOf(foo), bar: i32) i32 {
    if (bar > 0) {
        return foo1(bar - 4);
    }
    return bar;
}

fn a(comptime B: type) fn (B, i32) i32 {
    return opaque {
        fn f(b1: B, x: i32) i32 {
            if (x % 2 == 0) return b1(x / 2);
            return b1(x * 3 - 1);
        }
    }.f;
}

fn b(comptime A: type) fn (A, i32) i32 {
    return opaque {
        fn f(a1: A, x: i32) i32 {
            if (x % 3 == 0) return a1(x / 3);
            return a1(x * 5 - 1);
        }
    }.f;
}

const a_applied = a(@TypeOf(b(@TypeOf(a_applied))));

test {
    _ = foo;
    _ = a_applied;
}

$ zig test taiji-holes.zig
taiji-holes.zig:1:1: error: dependency loop detected
fn foo(foo1: @TypeOf(foo), bar: i32) i32 {
^~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
referenced by:
    test_0: taiji-holes.zig:29:9

C++: No.

#include <functional>

using FooFunc = std::function<int(FooFunc, int)>;
                               // ^ FooFunc is not defined

Lean: Sort of. A friend has pointed out that Lean has the refine tactic that deals with holes.

Function “coloring”

What is the “coloring” in “function coloring”? Note that the “coloring” here means totally different from the Taiji coloring above.

What is async fn(A) -> B?

Is it monad? A -> Future B

Is it effects? A -> <async> B

Analogous to how holes form in bread and cheese, let us call the nesting of bipolar regions in an algorithm “foamings”.

The function coloring simply comes from the fact that the language cannot treat types as regular values, plus it does not support native foaming.

Looking at async/await in Zig, the “async” effect has holes that implicitly receive a type as input:

xasync: fn (func, args, stack) Frame(ReturnType(@TypeOf(func)))

Therefore, we shall say that function coloring is an artifact of dependent types and foaming.

More colors, more symmetry groups

Why only two-fold symmetry $C_2$? If planar portals can be nested in a variety of ways, maybe algorithms can employ any symmetry group?

Placed here as a thought exercise.

Acknowledgement

The idea of monad comes from Idris 2.

The idea of algebraic effect comes from Koka.

The idea of nested regions of algorithm was originally expressed as part of a graphical algorithmic language, although the author called it “effects” and “holes” back then.

A discussion in the vague direction of LISP with screwlisp has prompted me to clarify the idea of nested regions.

A discourse of 玄 in the book《太玄》discuss about the development of real life events under a ternary system. It is safe to say that I do not understand that book.